LO-Net:Deep Real-time Lidar Odometry

LO-Net: Deep Real-time Lidar Odometry

用图像信息做位姿估计的深度学习方法近两年工作开始出现并且在一定的条件下取得了不错的效果，如《UnDeepVO: Monocular Visual Odometry through Unsupervised Deep Learning》（2017）是一种名叫UnDeepVO的新型单目视觉里程计系统，它可以可以估计单目相机的6自由度位姿以及使用深度神经网络估计单目视角的深度；

《PoseNet: A Convolutional Network for Real-Time 6-DOF Camera Relocalization》（ICCV 2015）是首次将deep learning和SLAM进行结合的文章，该方法使用 GoogleNet 做了 6自由度相机pose 的regression

《VINet: Visual-Inertial Odometry as a Sequence-to-Sequence Learning Problem》（2017）结合了惯导信息，做序列到序列的位姿学习，加入惯导信息可以整合惯导的优势帮助视觉估计出位姿；

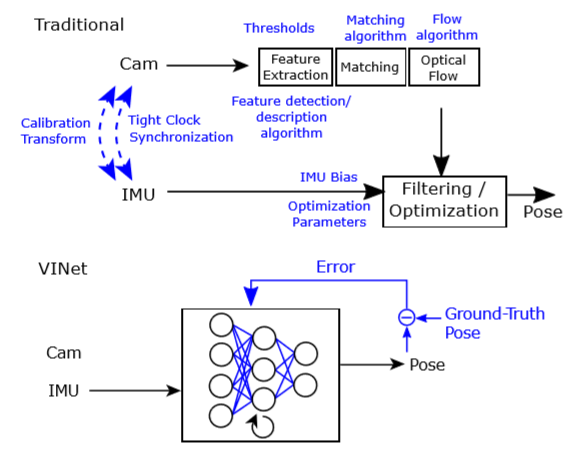
《Sfm-Learner: Unsupervised learning of depth and ego-motion》是google在2017年提出的利用连续几帧的序列作为输入，即用到了连续帧之间的对应点变换关系去估计出里程计的位姿变换和得到深度图，文章的核心思想是利用photometric consistency原理来估计每一帧的depth和pose。photometric consistency就是对于同一个物体的点，在不同两帧图像上投影点，图像灰度应该是一样的。

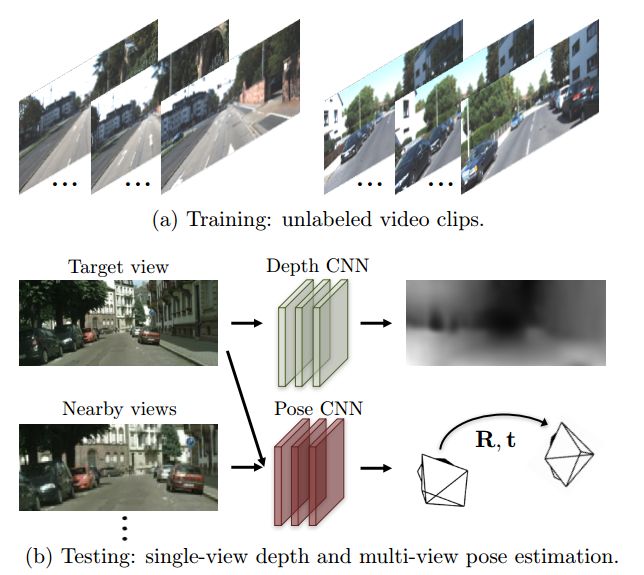
后续google基于sfm-learner提出了它的改进版《Sfm-Net:Learning of structure and motion from video》能做到从视频中学习运动估计，论文的核心思想也是利用photometric constancy来计算pose，depth。除此之外，作者还计算了光流，scene flow，3D point cloud等。

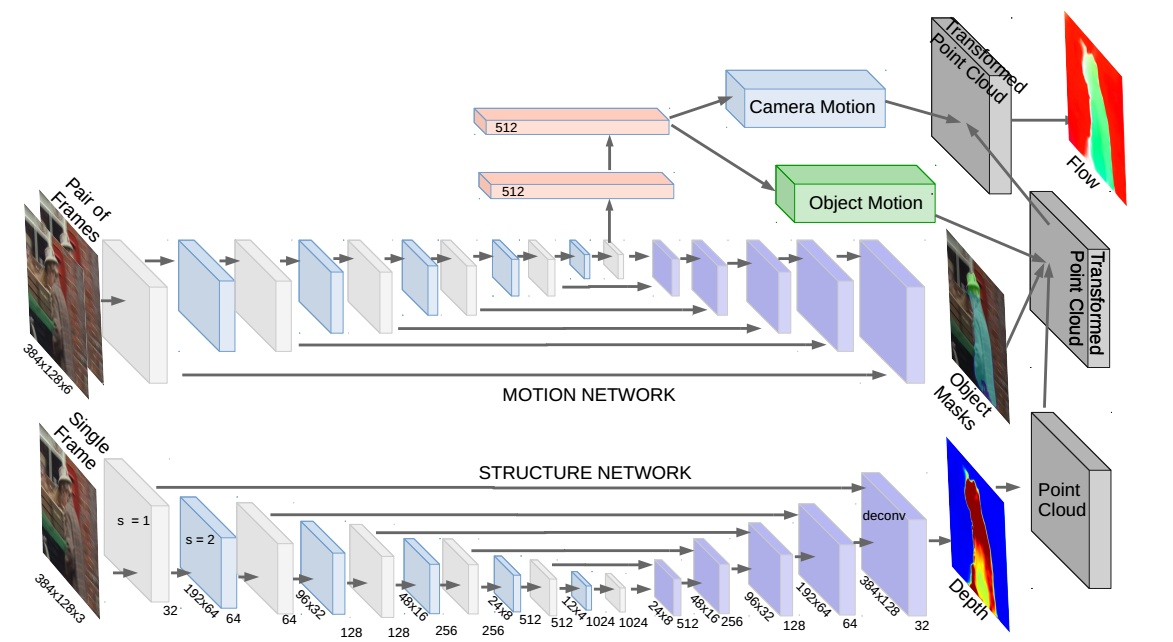
另外一篇和SfM-Net，SfM-Learner比较相似的文章：《DeMoN: Depth and Motion Network for Learning Monocular Stereo》（CVPR2017），使用pose, depth作为监督信息，来估计pose和depth。

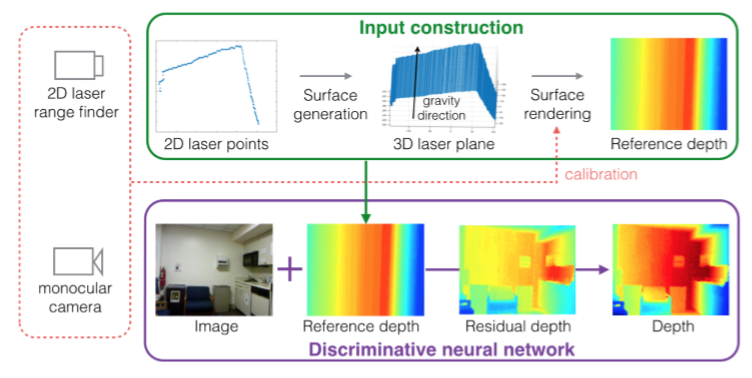
对于图像和激光融合的方法，目前有使用部分激光观测的单目深度估计《Parse Geometry from a Line: Monocular Depth Estimation with Partial Laser Observation》,这里的激光是单线的2D激光数据，激光在这里主要是为单目视觉信息补充深度所用

目前对于纯激光信息结合深度学习做位姿估计的工作还很少，在这里介绍一篇19年发表在CVPR上的文章LO-Net。

现在大多数现有的激光雷达位姿估计的方法都是通过单独设计特征选择、特征匹配和位姿估计的框架，然后分步将他们结合起来，并没有实现端到端的打通，本文章的一个工作是提出了一种端到端的lidar odometry estimation的框架，并且它的的思想借鉴了sfm-learner，利用了前后两帧的sequence去做LO估计。

先介绍一下文章的框架

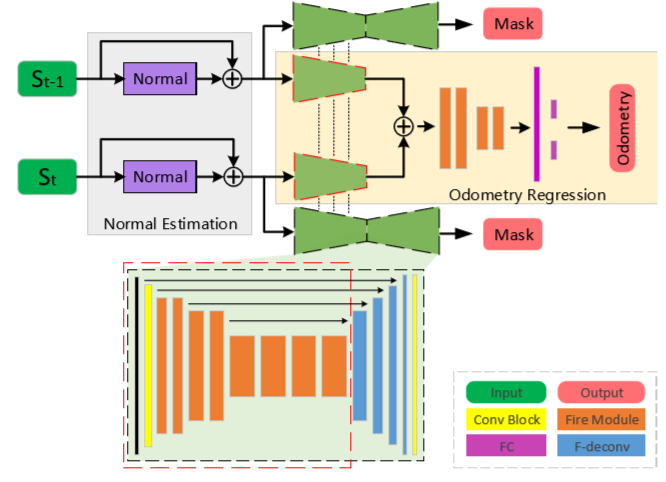
这个网络包含法向量估计、Mask预测子网络和位姿回归三个部分。网络用相邻两帧的点云作为输入，记为($S_{t-1}$;$S_{t}$)，输出为激光雷达的Odometry pose，这里的位姿并不是相对于全局坐标系（初始点坐标系）的，只是前一时刻相对于后一时刻来说的，对此文章后续还提出了利用lidar mapping对LO-Net的输出进行refne，最终得到关于世界坐标系下pose。另一部分输出还有Mask，这里的Mask（$\in [0,1]$）指的是该帧中具有空间一致性的概率，主要目的是区分出动态物体（如车辆和行人等）和静态场景。在某一个场景中，动态物体越多，代表其空间一致性越弱，因为这些动态物体会影响特征的提取。接下来分块具体解释这个网络：

• Lidar data encoding

  本网络并不是直接使用点云的坐标信息，而是对点云数据做了预处理，将其投影到了二维平面上，目的是为了让原始稀疏无规则的点云变得结构规范化。对于投影规则，文章作者引用借鉴的《Multi-view 3d object detection network for autonomous driving》（CVPR2017）文章里的方法：

  Given a 3D point p = (x,y,z) in lidar coordinate system(X,Y,Z), the projection function is: $\begin{split} \alpha &= \arctan(y/x)/\Delta \alpha \\ \beta &= \arcsin(z/\sqrt{x^2+y^2+z^2})/\Delta \beta \end{split}\tag{1}$ where $\alpha$ and $\beta$ are the indexs which set the points’ positions in the matrix. $\Delta \alpha$ and $\Delta \beta$ are the average angular resolution between consecutive beam emitters in the horizontal and vertical directions, respectively.

  运用这个方法可以将三维点云投影到一张$1800\times64$的二维图$(\alpha, \beta)$上，如果存在多个点投影到了一个位置，那么选取里激光雷达最近的点作为操作点。$(\alpha, \beta)$中的元素包含intensity值和对应空间点的range值 ($r = \sqrt{x^2+y^2+z^2}$)。文章里有个说法不能理解：

  “After applying this projection on the lidar data, we get a matrix of size $H\times W\times C$, and $C$ is the number of matrix channels. An example of the range channel of the matrix is shown in Figure 9.”

  

• Geometric consistency constraint

  Normal estimation

  

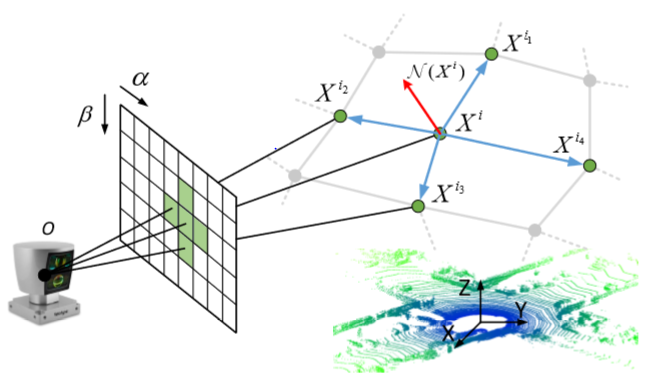
  对于法向量的估计，一般来说，为对于一个给定的三维点$X^i$和它的$k$个临近点$X^{i_j}, j=1,2,…,k$，法向量可以用下面约束函数估计： $arg\min_{\mathcal{N}(X^i)}\|[w_{i1}(X^{i_1}-X^i),...,w_{ik}(X^{i_k}-X^i)]^T\mathcal{N}(X^i)\|_2 \tag{2}$ 其中$w_{ik}$是$X^{i_k}$关于$X^i$的权重，为$\exp(-0.2|r(X^{i_k})-r(X^i)|)$，这个式子说明离目标点的距离越近，更有相似的局部空间结构，对应的权重越高。作者认为直接优化这个函数得到法向量$\mathcal{N}(X^i)$会影响计算效率，所以用最近的四个点作为邻域点，直接通过加权求和的方式近似得到这个法向量： $\mathcal{N}(X^i) = \sum_{X^{i_k},X^{i_j}\in \mathcal{P}}(w_{ik}(X^{i_k}-X^i)\times w_{ij}(X^{i_j}-X^i)) \tag{3}$ 其中${X^{i_1}, X^{i_2}, X^{i_3}, X^{i_4}}$按逆时针选取。

  激光雷达扫描应该是有前后帧的时间关联性和空间上的一致性，两帧之间的点应该有对应关系，现在令$X_{t-1}^{\alpha \beta}$和$X_{t}^{\alpha \beta}$为$t-1、t$连续两帧时刻投影矩阵$S_{t-1}、S_t$的元素，同时我们还能由两帧之间的转移矩阵得到$\hat{X}_t^{\alpha \beta}$: $\hat{X}_t^{\alpha \beta} = PT_tP^{-1}X_{t-1}^{\alpha \beta} \tag{4}$ 其中$T_t$是两帧之间相对刚体位姿变换，$P$和$P^{-1}$代表投影操作和它的逆。可以看到$X_t^{\alpha \beta}$和$\hat{X}_t^{\alpha \beta}$分别是通过设备扫描再投影得到和通过前一帧原始点云旋转平移再投影得到的，它们之间有差异，点不完全相同，并且即便是同一位置的点，因为变换矩阵的误差，也可能会出现该点的投影位置对应不上的问题，所以通过引入某一种相似性计算公式来约束调整pose。可以通过比较法向量$\mathcal{N}$来达到约束pose的目的，因为法向量有能反应光滑表面布局和边界结构的特点。 $\mathcal{L}_n = \sum_{\alpha \beta}\|\mathcal{N}(\hat{X}_t^{\alpha \beta})-\mathcal{N}(X_t^{\alpha \beta})\|_1\cdot e^{|\nabla r(\hat{X}_t^{\alpha \beta})|} \tag{5}$ 这里的$\nabla r(\hat{X}_t^{\alpha \beta})$是一种局部范围平滑操作，$\nabla$是一个关于$\alpha$和$\beta$的微分算子，用到这个是因为一阶、二阶导数都是突出边界较好的操作，加上$e^{|\cdot|}$是为了让loss function更大程度的关注到sharply changeing area。

• Lidar odometry regression

  在网络中，经过了normal estimation部分后，将估计到的normal放到二维投影图中，即图中每个位置的值用对应空间点的vector赋值，$S_{t-1}$和$S_t$分别有两条线路同时进入特征提取网络中

  

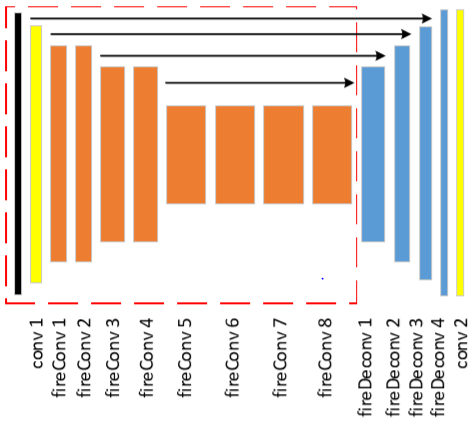
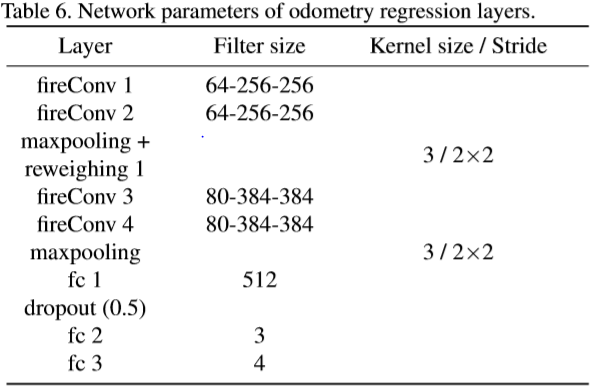
  红框所包含的内容为特征提取部分，这里的橘黄色对应的层不是卷积层，作者引用了SqueezeNet《SQUEEZENET: ALEXNET-LEVEL ACCURACY WITH 50X FEWER PARAMETERS AND <0.5MB MODEL SIZE》（ICLR2017）文章中提出的FireConv用来减少计算复杂度和模型参数

  

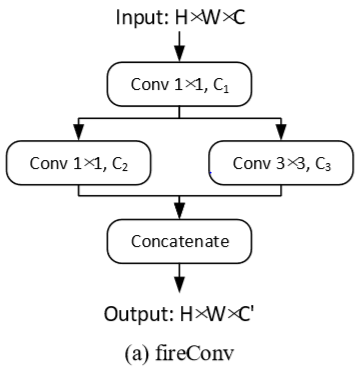
  第一个$1\times1$的卷积操作目的是压缩input tensor，第二个$1\times 1$卷积和$3\times3$卷积帮助网络从两个尺度学习到更多的特征。接下来将两条线的feature concatenate在一起再进入回归层，最后两个并列的全连接层分别是3维和4维的平移$x$和四元数旋转$q$，整体来看，经过最后的三个全连接层输出两帧之间6自由度的pose。

  

  Learning position and orientation simultaneously

  在本文章中，使用四元数来代表旋转。因为四元数$q$和旋转矩阵$R$之间转换满足罗德里格斯公式，可以发现$q$和$-q$表示相同的旋转，所以我们需要将其限制在一个半球上。使用$\mathcal{L}x(S{t-1};S_t)$和$\mathcal{L}q(S{t-1};S_t)$分别表示如果去学习两帧之间相对平移和旋转： $\begin{split} \mathcal{L}_x(S_{t-1};S_t) &= \|x_t-\hat{x}_t\|_l \\ \mathcal{L}_q(S_{t-1};S_t) &= \|q_t-\frac{\hat{q}_t}{\|\hat{q}_t\|}\|_l \end{split}\tag{6}$ 其中$x_t、q_t$是groudtruth，$\hat{x}_t、\hat{q}_t$是对应的预测值，以及在这里$l$取2。由于平移和旋转之间存在尺度和单位不一致性，以往的方法是给旋转loss一个权值规范因子$\lambda$，在这里作者认为这个超参数需要随着场景数据的分布而不断细调，在这里作者使用两个可学习的参数$s_x$和$s_q$去平衡两者的尺度： $\mathcal{L}_0 = \mathcal{L}_x(S_{t-1};S_t)\exp{(-s_x)}+s_x+\mathcal{L}_q(S_{t-1};S_t)\exp{(-s_q)+s_q} \tag{7}$ $s_x$和$s_q$的初始值为$s_x = 0.0$和$s_q = -2.5$。

• Mask prediction

  激光雷达点云被认为能表示场景的3D信息，当然也会包含一些动态物体如车辆和行人，这些动态物体有时会妨碍位姿回归网络的学习，文章利用《Unsupervised Learning of Geometry with Edge-aware Depth-Normal Consistency》和《 Unsupervised learning of depth and ego-motion from video》（CVPR2017）两篇文章的思路，加入了Mask模块，去学习动态物体的补偿(这里是直译过来的，没能理解作者的意思)，并且能提高特征学习的有效性和鲁棒性。Mask prediction和odometry regression的特征提取部分网络是参数共享的，可以联合同时学习两个网络。对于Mask prediction部分的deconvolution层，采用FireDeconv，并且在网络中加入了skip connection。

  

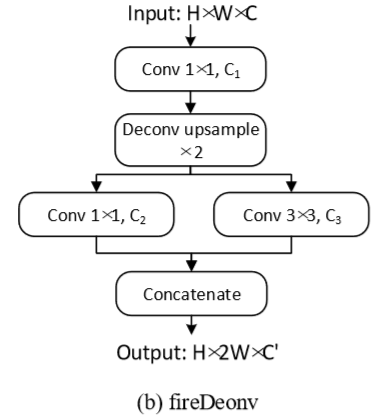
  Mask prediction的网络如下图所示

  

  这里解释一下maxpooling+reweighing层和enlargement+reweighing层，这个概念实则出自文章的参考文献《Pointseg: Real-time semantic segmentation based on 3d lidar point cloud》。先进行一次maxpooling，只对Width进行降采样，所以这里的Stride为$1\times2$，再紧接着做如下示例的reweighting操作

  

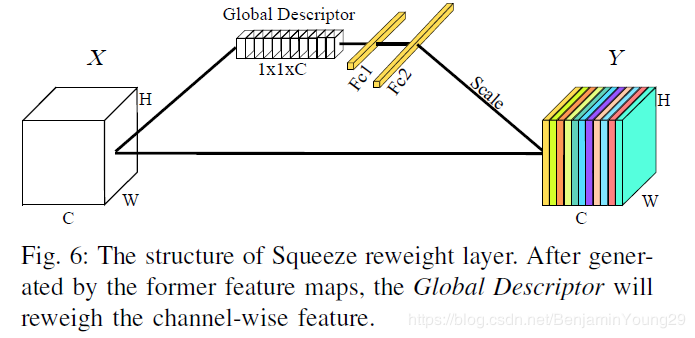
  对于每一个channel的feature map用平均pooling去得到一个全局的描述信息

$$\begin{split} \mathcal{X}_n &= \frac{1}{H\times W}\sum_{i=1,j=1}^{H,W}p_n(i,j), n\in C \\ X_n &= sigmoid(\mathcal{X}_n) \\ Y_n &= X_n \cdot Scale_n , n\in C \end{split} \tag{8}$$

对于enlargement+weighing层，思路和maxpooling+weighing是一样的，只是enlargement采用空洞卷积层来扩大感受野而不是池化

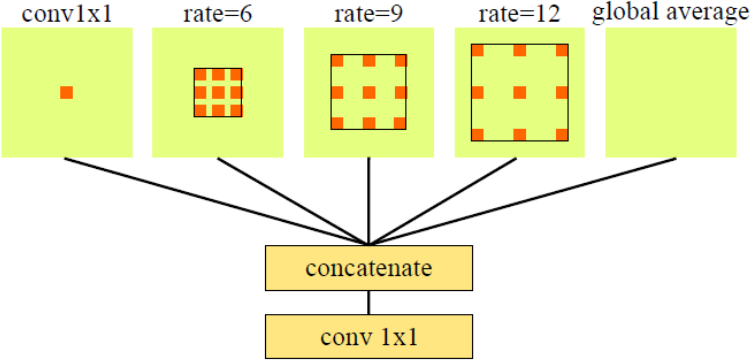
通过上面的操作得到了predicted mask $\mathcal{M}(X_t^{\alpha \beta})\in [0,1]$，这个说明此点附近区域是否有空间一致性（可以理解为是否为动态物体），也代表了特征的可靠程度(reliability of the feature)，将$\mathcal{M}(X_t^{\alpha \beta})$加到式（5）中得到 $\mathcal{L}_n = \sum_{\alpha \beta}\mathcal{M}(X_t^{\alpha \beta})\|\mathcal{N}(\hat{X}_t^{\alpha \beta})-\mathcal{N}(X_t^{\alpha \beta})\|_1 \cdot e^{|\nabla r(\hat{X}_t^{\alpha \beta})|} \tag{9}$ 因为这个过程没有标签和监督信息，所以网络有可能会通过把$\mathcal{M}$设为0以最小化$\mathcal{L}_n$，所以为了避免这个情况，加入一个互信息loss作为正则项： $\mathcal{L}_r = -\sum_{\alpha \beta}\log{P(\mathcal{M}(X_t^{\alpha\beta})=1)} \tag{10}$ 最终，整个odometry regression部分的loss为 $\mathcal{L} = \mathcal{L}_0 + \lambda_n\mathcal{L}_n + \lambda_r\mathcal{L}_r \tag{11}$ 这里$\lambda_n$和$\lambda_r$为权重系数，是预先设置的超参。

• Mapping: scan-to-map refinement（本部分需要更多时间去了解细节，目前有些部分还是没搞懂）

  最后一部分为mapping，本文章用到mapping除了建图还有用mapping来精调里程计位姿。我们之前所讨论的情况都是两帧之间的相对变换，经过一段时间的误差累计后，里程计会有漂移。另一个方面，相邻帧点云之间相同的特征点毕竟有限，没有累积建立起的图那么丰富（这里我认为主要考虑的是回环的情况）。本文章运用map和当前scan之间的匹配去做精调(refine)，（1）使用法向量信息从smooth area选点 （2）用mask排除掉移动物体的点。

  在$t$时刻，$[T_t, S_t]$是从LO-Net得到的数据，$T_t$是odometry，用来做mapping的初始位姿。$S_t$是包含intensity, range, normal and mask value of each point等信息的多通道数据矩阵。

  

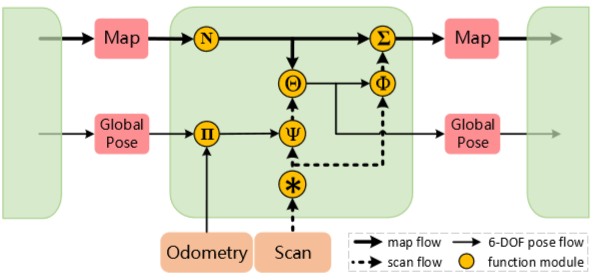
  用Odometry和Scan作为输入，经过中间这个模块的操作，能得到更新后的map和全局pose。

  • * 操作：基于$S_t$的normal通道，通过定义下面这个式子去评估局部区域的平滑性 $c = \sum_{k=1}^3(K*\mathcal{N}_k)^2 \tag{12}$ $\mathcal{N}_k$是$S_t$的某一个点对应法向量通道的特征向量。对于$K$，$K$是一个$3\times5$的卷积核，它的中心值为-14，其余14个点的值为1。通过式（12）算得每个点的$c$，再将$S_t$所有点的$c$进行升序排序，选取除mask标记的前$n_c$个点，这些点实则也代表光滑平面上的点。

  • $\bf{\Pi}$：Compute an initial estimate of the lidar pose relative to its first position: $M_{init} = M_{t-1}M_{t-2}^{-1}M_{t-1}$, where $M_t$ is the lidar transformation at time t.

    我认为应该是$M_{init} = M_{t-1} T_t$，即t-1时刻的全局变换乘上t-1和t之间的相对变换，作为t时刻的初始全局变换

  • $\bf{\Psi}$：通过用$T_t$的线性插值对自运动进行补偿来消除由$S_t$得到的点云运动畸变，然后使用$M_{init}$将纠正的$S_t$变换到全局坐标系中，准备匹配。

    假设 $\bf{p}_i = (p_{i_x}, p_{i_y}, p_{i_z},1)^T$ 是 $S_t$ 中的一个点，$\bf{m}_i = (m_{i_x}, m_{i_y}, m_{i_z}, 1)^T$ 是由之前t-1个时间点建立起来图中的某个对应点，$\bf{n}_i = (n_{i_x}, n_{i_y}, n_{i_z}, 0)^T$ 是 $\bf{m}_i$ 的单位法向量。mapping的目标是找到一个最优的刚体变换： $\hat{M}_{opt} = arg\min_{\hat{M}}\sum_i((\hat{M}\cdot \bf{p}_i -\bf{m}_i)\cdot \bf{n}_i)^2 \tag{13}$

• $\bf{\Theta}$：通过解式（13）不断迭代得到多个匹配变换$\hat{M}_k$直到达到最大的迭代数$n_{iter}$，最后将这些$\hat{M_k}$按先后顺序乘起来最后乘上初始值$M_{init}$得到最终的变换$M_t$ ： $M_t = \prod_{k=1}^{n_{inter}} \hat{M}_kM_{init} \tag{14}$

  • $\bf{\Phi}$：通过对$M_{t-1}$和$M_t$之间的车辆运动进行线性插值从当前场景$S_t$形成新的激光点云。
  • $\bf{\Sigma}$：将这个新的点云加到map中形成更新的map。
  • $\bf{N}$：移除掉比较早时刻的点云帧，只为map保留$n_m$个scans（因为本文章只涉及odometry，没有建图，所以有这一步操作）

最后是实验展示部分，作者在实验的时候选取的input sequence是3。$\lambda_n$和$\lambda_r$分别取的0.15和0.05，学习率取得0.001, batch_size = 8，$n_c = 0.01 H\cdot W$，$n_m = 100$，$n_{iter} = 15$。比较的方法为ICP-point2point, ICP-point2plane, GIP, CLS, LOAM and Velas。